SOLUCIÓN EXAMEN MAS Y ONDAS 2º BACHILLERATO

1.      Ejercicio sobre péndulo físico: Un péndulo físico de 3 metros de largo oscila en un lugar de la Tierra en el que g=9,79 m/s². ¿Cuál es el período de oscilación? ¿Y su frecuencia? [0,5 cada respuesta correcta; 0,5 dibujo y planteamiento; 0,5 unidades]

 2.      Ejercicio sobre ondas estacionarias: Una onda estacionaria en una cuerda de 1,5 metros de larga tiene la siguiente ecuación: y(x,t)=10sen(2πx)cos(πt).

a.      Escribe la ecuación de las ondas que la originaron. E indica la longitud de onda y pulsación de tales ondas. [0,5 ecuación y 0,5 parámetros]

b.      ¿Qué armónico se formó? ¿Cómo se podría formar el fundamental? [0,25 cada correcta, 0,5 razonamiento-redacción]

c.       ¿Por qué una onda estacionaria no es una onda [0,5 correcto; 0,5 redacción]

Cuando tenemos dos ondas idénticas, pero trasladándose en sentido opuesto en la misma dirección, pueden superponerse en una región del espacio dando lugar a las ondas estacionarias. Para obtener la expresión de las ondas estacionarias debemos sumar dos senos de ángulos, (fases), distintos.

Sin que podamos a partir de los datos conocer la fase inicial de las ondas originarias.

En cuanto a la segunda cuestión, al ser la distancia que hay entre dos nodos consecutivos media longitud de onda, en nuestro caso λ=1 metro, por tanto estamos hablando de 0,5 metros, y como la cuerda mide 1,5 metros, deducimos que hay 4 nodos. Y por tanto tres vértices, lo que significa que estamos ante el tercer armónico.

Si deseáramos tener el estado fundamental tendríamos dos opciones excluyentes: o las ondas generadoras de las estacionarias son de longitud de onda 3 metros, o la cuerda sólo mide 0,5 metros para unas ondas de λ=1m.

c) La interferencia de dos ondas idénticas que se propagan en sentido opuesto produce las ondas estacionarias. En realidad la Onda estacionaria no es una onda como tal, sino un conjunto de osciladores alineados vibrando en sentido transversal a la onda origen, cada uno con una amplitud distinta del contiguo según su posición en el espacio.

Su ecuación es la correspondiente a un MAS de una partícula situada en punto "x", en cuya amplitud interviene el factor cos(kx)  y así cada partícula tendrá una amplitud dependiendo de la posición en la que se encuentren.

Se llama estacionaria debido a que no hay transporte de energía, ya que esta queda almacenada entre los nodos, donde las partículas están en reposo, y no trasmiten la energía.

3.      Tema de redacción: Define Intensidad de ondas y explica por qué en el caso de las ondas esféricas, la intensidad disminuye con la distancia. [0,5 definición; 0,5 explicación correcta sobre relación con la distancia]

La intensidad de la onda es la cantidad de energía que atraviesa la unidad de superficie en la unidad de tiempo.

La intensidad disminuye con la distancia en el caso de ondas esféricas propagándose por medio homogéneos e isótropos debido al hecho de que la energía que transporta la onda es siempre la misma, pero se debe repartir en frentes de onda cada vez más amplios. Los frentes de ondas en las ondas esféricas son esferas de radio r, centrada en el punto donde se generan. Por tanto su superficie es 4πR², siendo R el radio de la esfera.

Supongamos que tenemos dos frentes de ondas de radios R₁ y R_2, (R₁2), la superficies de las esferas serían: S₁=4πR²₁    S₂=4πR²₂. La energía que contiene cada frente de onda sería la misma, la llamamos E, entonces la intensidad en cada frente de onda vale:

I₁=E/(tS₁)=(E/t·4π)·1/R₁ ² =cte/ R₁ ²               I₂=E/(tS₂)=(E/t·4π)·1/R₂ ² =cte/ R₂ ²

Y al ser R2 mayor que R1, entonces, la intensidad I2 es menor que I1.

4.      Demostración: Un MAS se rige por una ecuación del tipo y(t)=A·cos(wt), suponiendo que no hay fase inicial.

a.      Encuentra las expresiones de la velocidad y la aceleración en función del tiempo (1 OK)

b.      Encuentra las expresiones de la velocidad y la aceleración en función de la posición (1 OK)

c.       Encuentra que la energía total en un MAS es un valor constante.

Si partimos de un movimiento armónico descrito por la ecuación y(t)=A·cos(wt) para encontrar la velocidad y aceleración en función del tiempo para este movimiento no tenemos más que derivar:

V(t)=dy/dt=-A·w·sen(wt)           a(t)=dv/dt=-Aw²cos(wt)

Podemos eliminar el tiempo en las expresiones anteriores, relacionando directamente velocidad y aceleración con la posición del objeto oscilante. Para la aceleración es muy sencillo, sin  más que comparar ambas expresiones a(t) y y(t), llegamos a la conclusión …

a(y)= -w²·y

Para la velocidad debemos aplicar la conocida relación entre seno y coseno:

Sen²(Z)+Cos²(Z)=1

Sen(Z)=RAIZ(1-Cos²(Z))

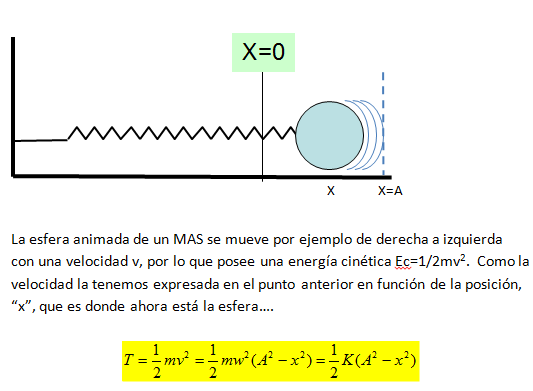
Demostremos ahora que la energía en un MAS es constante. Cuando el objeto esté oscilando en torno a su posición de equilibrio dispondrá de energía potencial y energía cinética:

La última igualdad la podemos escribir porque por definición w²=K/m. Por otra parte la esfera también posee una energía potencial por estar situada en “x”. Su valor es:  Ep=1/2 Kx²

La energía total es la suma de la energía potencial y de la energía cinética:

E_total=Ec+Ep=1/2 K(A²-x²)+1/2Kx²=1/2KA²

En esta expresión no interviene ni el tiempo ni la posición que ocupa la esfera,  tenemos entonces un valor constante para la energía total, que depende únicamente de la constante del muelle y de la amplitud del movimiento.

  

5.      Definición: ¿Qué son las oscilaciones amortiguadas? ¿Por qué se producen? [0,5 definición; 0,5 causa de ellas bien expresado]

Los movimientos oscilatorios en la realidad están amortiguados, con el tiempo van perdiendo amplitud, hasta que cesan. Esto es debido a los rozamientos de todo tipo que tienen lugar, que van secuestrando energía al sistema y al ser la energía proporcional al cuadrado de la amplitud esta va disminuyendo con el tiempo.