1. Dibuja el campo magnético creado por …
a)
Un
hilo conductor rectilíneo infinito por el que circula corriente eléctrica.
b)
Un
solenoide lineal formado por muchas espiras a su largo.
Aquí podéis ver las líneas del primer caso, con la regla de
la mano derecha que nos permiten deducir el sentido de ellas. (Obtenido de https://eluniversomatematicoblog.wordpress.com/2017/11/19/campo-magnetico-debido-a-una-corriente-rectilinea/)
2.
Demuestra
con ayuda del Teorema de Ampere la expresión del campo magnético de un
solenoide. (Fíjate en el criterio de calificación)
Tenemos
aquí representado un solenoide, de longitud L, con N vueltas, por el que
circula una corriente I. Dibujamos en línea ACDE cerrada y aplicamos el Teorema
de Ampere:
 |
Cálculo de la corriente encerrada:
Sea N el número de espiras, y L la longitud del
solenoide Si la corriente que circula por cada espira es I, entonces la
corriente total encerrada por la espira amperiana N veces la intensidad que
circula por cada espira:
Ienc=N·I
Aplicación del Teorema de Ampère y obtención de la
expresión:
Sustituyendo los resultados de la integral de línea y
la corriente encerrada en el teorema de Ampère:
B·L=μ0N·I
Dividiendo ambos lados por l, obtenemos la expresión
para la magnitud del campo magnético dentro del solenoide:
B=μ0N·I/L
3.
¿Cuál
es la causa de la existencia de magnetismo en la materia a nivel
atómico-molecular? Describe la respuesta y no contestes con una única palabra o
similar.
La existencia del magnetismo en la materia a nivel
atómico-molecular tiene su origen fundamental en el movimiento de los
electrones dentro de los átomos y en una propiedad intrínseca de estas
partículas llamada espín. No se trata de una única causa, sino de la
combinación de estos dos fenómenos cuánticos:
- Movimiento orbital de los electrones: Los electrones, al orbitar alrededor del núcleo atómico, generan una corriente
eléctrica a nivel microscópico. De acuerdo con las leyes del
electromagnetismo, toda corriente eléctrica produce un campo magnético.
Por lo tanto, cada electrón en movimiento orbital actúa como un diminuto
electroimán, generando un momento dipolar magnético orbital. La
magnitud y dirección de este momento magnético dependen del momento
angular orbital del electrón.
- Espín del electrón: Además de su
movimiento orbital, el electrón posee una propiedad cuántica intrínseca
llamada espín, que no tiene una analogía clásica directa con un
objeto girando. El espín también está asociado a un momento dipolar
magnético intrínseco, conocido como momento magnético de espín.
Se comporta como si el electrón fuera una pequeña aguja imantada.
(respuesta obtenida con IA, Gemini)
4. A continuación tienes las 4 ecuaciones de Maxwell, responde a las siguientes preguntas.
a.
¿Cuáles están
relacionadas con el Teorema de Gauss?
b.
¿qué consecuencia
física tienen las otras ecuaciones no contempladas en la pregunta (a)?
De nuevo
respuesta obtenida por IA (Gemini). Las ecuaciones de Maxwell que están
directamente relacionadas con el Teorema de Gauss son la Ley de Gauss
para el campo eléctrico (1) y la Ley de Gauss
para el campo magnético (2).
Las otras dos ecuaciones de Maxwell, que no están directamente relacionadas
con el Teorema de Gauss, tienen profundas consecuencias físicas:
- Ley de
Faraday-Lenz (3): Esta ley describe el fenómeno de la inducción electromagnética.
Establece que un campo magnético variable en el tiempo induce un campo
eléctrico. Este principio es fundamental para el funcionamiento de
generadores eléctricos, transformadores y muchas otras tecnologías.
- Ley de
Ampère-Maxwell (4): Predice que un campo eléctrico variable en el tiempo también genera
un campo magnético, de manera análoga a como una corriente eléctrica lo
hace. La consecuencia más importante de esta ley es la predicción de la
existencia de ondas electromagnéticas
5. Tres conductores paralelos infinitos se sitúan sobre los vértices de un triángulo rectángulo de 8 metros de cateto. El que se sitúa en el ángulo recto transporta una corriente eléctrica de 4 A, mientras que los otros dos llevan 2 A. Y todos en el el mismo sentido.
a.
Calcula el campo
magnético creado por los tres conductores en el centro de la hipotenusa.
b. Calcula la fuerza que los dos de los extremos crean
sobre el situado en el ángulo recto. EXPRESA EL RESULTADO VECTORIALMENTE.
En el dibujo podemos apreciar que la hipotenusa la podemos obtener con el
Teorema de Pitágoras, y obtenemos que d= 11’3 metros.
También he incluido los vectores campo magnético, de verde, obtenidos con
la regla de la mano derecha para dirimir sentido y dirección del vector.
Los módulos de las dos fuerzas son iguales, porque las intensidades son
iguales, así como las distancias, en la expresión de cálculo de la fuerza.
Recordemos que esa ecuación nos proporciona la fuerza por unidad de longitud de
conductor.
F=F1 + F3 = 2.03·10-7 i + 2.03·10-7 i (N/m)
Y
el módulo de la fuerza resultante, será el módulo de ese vector suma F= RAIZ{ (2.03·10-7)2 + (2.03·10-7)2 } = 2.82·10-7
N/m.
De
nuevo, en negrita los vectores.
6. Sobre un circuito cuadrado de 10 cm de lado y 20 espiras aplicamos un campo magnético perpendicular de 0,25 T, pero que disminuye en 0’01 segundos a 0,025 T.
a.
Describe
lo que le ocurre al circuito cuando se produce ese descenso de intensidad
magnética.
b.
Calcula
la fem inducida.
Cuando por el circuito hay un campo magnético de 0’25 T, y desciende a 0’025 T, el flujo magnético que atraviesa el circuito disminuye. El circuito responde generando una corriente inducida que intente compensar el flujo magnético que ha desaparecido.
7.
Una
espira circular de 5 cm de radio y 100 espiras mantiene una corriente eléctrica
de 0,25 A, cuando de repente hay un cortocircuito. ¿Qué ocurre al circuito en
los primeros instantes y cómo se llama ese fenómeno físico?
Algo parecido al problema anterior, la corriente mantiene un
campo magnético que atraviesa la espira. Por tanto, hay un flujo magnético de
valor “X”. Cuando cesa la corriente, el circuito responde creando una corriente
autoinducida que intenta que ese valor “X” del flujo se mantenga, aportando un
campo magnético inducido que reponga el flujo magnético perdido. Este fenómeno se denomina “autoinducción”.
8.
Completa
las siguientes descomposiciones radiactivas, señalando la partícula formada y
el núcleo “hijo” formado.
11. El
estroncio-90 es un isótopo radiactivo peligroso que se encuentra en los residuos
nucleares. Su periodo de semidesintegración es de 28.8 años.
a) Calcula la constante de desintegración radiactiva (λ)
del estroncio-90.
b) Si una muestra inicial contiene 3.5×1015
núcleos de estroncio-90, ¿cuántos núcleos quedarán después de 100 años?
c)
¿Cuál el valor de la actividad en unidades del SI en la muestra inicial?
Calcula la
energía de enlace por nucleón para el oxígeno-16 en MeV/nucleón. (Dato: 1
u.m.a. = 1.66054×10−27 kg, c=3×108 m/s, 1 eV = 1.602×10−19
J).
13. El
Modelo Estándar de física de partículas describe las partículas fundamentales
que componen toda la materia y las fuerzas que actúan entre ellas. Dentro de
este modelo, las partículas se dividen en dos grandes categorías según su
estadística cuántica: fermiones y bosones.
a) Explica
las principales diferencias entre fermiones y bosones en términos de su espín y
el principio de exclusión de Pauli.
b)
Identifica y clasifica, dentro del Modelo Estándar, dos ejemplos de fermiones y
dos ejemplos de bosones, indicando brevemente el papel fundamental que
desempeñan en la constitución de la materia o en la transmisión de las
interacciones fundamentales.
Los fermiones son partículas que poseen spin semientero, no pueden
existir en un sistema físico dos fermiones idénticos, se deben diferenciar en
algún valor físico, normalmente un número cuántico. Es lo que se conoce como
Principio de Exclusión de Pauli. Los fermiones dentro del Modelo Estándar son
las partículas que forman parte de la materia: quarks y electrones.
Al contrario de los fermiones, los bosones tienen spin entero, y esa
característica permite que en un sistema físico puedan existir varios bosones
idénticos. Los bosones en el Modelo Estándar son las partículas que portan las
interacciones en el Universo, son los fotones y gluones.







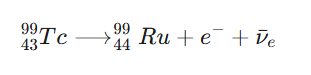

No hay comentarios:
Publicar un comentario