SOLUCIÓN EXAMEN 2BACH FÍSICA 23-24 ONDAS

 

1.      De un muelle colgado verticalmente colgamos una masa de 200 gramos alargándose 5 cm. Posteriormente tiramos de la masa unida al muelle hasta que se alarga 1 cm, dejándolo oscilar libremente. Suponemos que no hay amortiguamiento.

a)     Calcula la constante de elasticidad del muelle.

b)     Calcula la frecuencia de oscilación de la masa oscilante.

Sabemos que al colgar una masa de 200 g se alarga 5 cm, aplicamos directamente la ley de Hooke para calcular la constante de elasticidad del muelle:
 
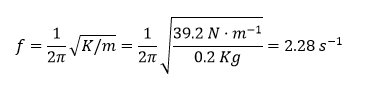
          F= K·Δx  à K=F/Δx=(m·g)/Δx=(0.2 Kg · 9.8 m/s²)/0.05 m = 39,2 N/m
 
Sabemos la relación que guarda K en un muelle con una masa oscilante con la frecuencia:
 w²=K/m       Y además w= 2·π·f

2.      TEORÍA (Una demostración matemática): Sabiendo que el movimiento de una masa “M” es gobernado por la siguiente ecuación del movimiento x(t)=A·sen(w·t), obtén:

a)     La ecuación de la velocidad en función del tiempo.

b)      La ecuación de la velocidad en función de la posición de la masa.

 Para encontrar la ecuación de la velocidad, no tenemos más que derivar la ecuación del movimiento:

V(t)=dx(t)/dt=A·w·cos(w·t)

Para obtener la ecuación de la velocidad en función de la posición, recurrimos a la relación trigonométrica: sen²(wt)+cos²(wt) = 1. De donde despejamos el coseno: cos(wt)=RAIZ(1-sen²(wt)). Y ahora sustituimos en la ecuación de la velocidad en función del tiempo obtenida antes:

Lo que hemos hecho tras la sustitución es introducir dentro de la raíz la amplitud, lógicamente al cuadrado, y multiplicar por los dos factores que estaban dentro de la raíz. De esta manera en sustraendo será la posición de la masa al cuadrado, y ya obtengo lo que buscaba.

 

3.      Dada la siguiente gráfica correspondiente a un fenómeno ondulatorio correspondiente a un punto en el origen, ….

a)     ¿Cuál es el período de la onda y su amplitud? Señala sobre la gráfica.

b)     ¿Tiene fase inicial? Razona tu respuesta, que es lo que puntúa.

c)      Si la onda pasara a moverse por otro medio, y entonces cambiara su velocidad de propagación “c”, ¿cambiaría su longitud de onda o su frecuencia? ¿Por qué?

Hemos señalado en la gráfica con flechas tanto la amplitud como el período. La amplitud será la mayor cantidad que se separe del punto de equilibrio la función de onda, y el período el tiempo que debe de pasar para que se repita el valor de la onda y su tendencia ascendente o descendente. La amplitud es “1”, y el período 2 segundos.

La onda sí tiene fase inicial porque en el foco, y en el instante inicial el valor de la función de onda es un valor distinto de cero. En este caso es π/2 al valer la función “1”.

Si cambia “c”, debe de cambiar la longitud de onda. La frecuencia va asociada al origen del fenómeno ondulatorio, con la frecuencia de los pulsos que provocan la aparición de la onda.

4.      Una onda mecánica correspondiente a las ondulaciones de una cuerda viene descrita con los siguientes parámetros, tiene una amplitud de 3 mm, se propaga con una velocidad de 3 m/s, tiene una longitud de onda de 1’5 m, y sabemos que en el punto origen de la onda, y en el instante inicial la posición de la cuerda estaba 3 mm por encima de la posición de equilibrio.

a)     Calcula el valor de la frecuencia, período, fase inicial, k, w.

b)     Escribe la ecuación de la onda con sus valores numéricos para este caso.

c)      Para un punto de la cuerda situado a 0,75 metros del origen, obtén la ecuación de su movimiento armónico simple.

d)     Calcula la distancia que hay entre dos puntos de la cuerda que en el mismo instante de tiempo, mantienen una diferencia de fase de π radianes.

 

a)      Calculamos el valor de K=2π/λ=2π/1.5m=4π/3 m^-1. Ahora que sabemos lambda, calculamos la frecuencia:

f=c/λ=3ms^-1/1.5m=2 s^-1.

El período es inmediato T=1/f=0.5 s, al igual que w=2πf=4π s^-1.

Para calcular la fase inicial, sabemos que en t=0s, y x=0s, ψ(0,0)=3 mm. Planteamos lo que sabemos de cómo sería la ecuación de onda:

Ψ(x,t)= A·sen(kx-wt+ϕ₀) = 3·sen( 4π/3 x - 4πt + ϕ₀)

Y damos valores nulos a posición y tiempo, sabiendo que el resultado sería 3 mm:

Ψ(0,0)= 3·sen(ϕ₀)=3

El seno debe valer “1”, lo cual ocurre cuando ϕ₀=π/2

 b)      La ecuación de onda resulta ser: Ψ(x,t)= A·sen(kx-wt+ϕ₀) = 3·sen( 4π/3 x - 4πt + π/2) (mm)

c)      Un punto de la cuerda cualquiera, tendrá un M.A.S. con la amplitud y LA frecuencia angular heredadas de la onda. Pero cada punto tendrá unA fase inicial distinta del resto. Por tanto, de entrada la ecuación del movimiento será:

Y(t)=3·sen(4πt+ϕ₀)

Debemos calcular la fase inicial y ya lo tendríamos. Primero calculemos el tiempo que tarda la onda en llegar a ese punto de la cuerda. Ese instante será el último en el que ese fragmento de cuerda no vibre, y esté por tanto en la posición y(t)=0 mm

 Tiempo = Posición del punto/ Velocidad de la onda = 0.75 m /3 ms^-1=0.25 s

A los 0.25 segundos abandona su estado de reposo, que es el tiempo que tarda la onda en llegar a él desde el origen, moviéndose a 3 m/s.

 Aplicamos lo dicho en el párrafo superior: y(0.25s)=0mm=3·sen(4π·0.25 + ϕ₀).

El seno debe valer 0, es decir que el argumento de la función ha de ser cero: 4π·0.25 + ϕ₀=0

Despejamos y ϕ₀=-π.

Ecuación de movimiento del punto de la cuerda situado en x= 0.75m: Y(t)=3·sen(4πt-π)

 d)      Calculamos la distancia entre puntos que en un instante mantienen una diferencia de fase de π radianes. Estos puntos estarán situados en x₁ y x₂, y el instante de tiempo será “t”. La ecuación de la onda, recordémoslo es Ψ(x,t)= 3·sen( 4π/3 x - 4πt + π/2)

FASE DEL PRIMER PUNTO: 4π/3 x₁ - 4πt + π/2         FASE DEL SEGUNDO PUNTO: 4π/3 x₂ - 4πt + π/2

Restamos los valores, sabiendo que el resultado es π radianes.

(4π/3 x₂ - 4πt + π/2)-( 4π/3 x₁ - 4πt + π/2)=π

4π/3 (x₂-x₁)=π  

(x₂-x₁)=3/4 metros.

 

5.      Un trueno asociado a un rayo producido en una tormenta tiene una potencia de 50 millones de wattios en el origen.  Supongamos que las ondas sonoras se propagan en todas las direcciones por igual, y sin absorción.

a)     Calcula la intensidad del sonido a 10.000 metros de distancia.

b)     ¿Cuál será la RELACIÓN ENTRE LAS AMPLITUDES DE LAS ONDAS en los frentes de ondas situados a 1.000 metros y 10.000 metros del origen respectivamente?

c)      ¿Cuál es la sonoridad en decibelios a 10.000 metros del origen del rayo? Dato: Intensidad física umbral I₀=10^-12 Watt/m²

La intensidad se define como el cociente entre la potencia y la superficie del frente de onda, que en este caso supondremos esférico, y por tanto S=4πR².

I=Pot/4πR²=50·10⁶ Watt/(4π10.000²m²)=(5/40π)· watt/m²=0.040 watt/m²

Ahora buscamos la relación que hay entre las amplitudes, no buscamos el valor de cada amplitud, sólo la relación:

R₂/R₁ =A₁/A₂ à A₁/A₂ =10.000 m/1.000 m = 10 veces es mayor A₁ que A₂

Finalizamos con la sonoridad S=10log(I/I_umbral)=10·log (0.040 watt·m^-2/10^-12 watt·m^-2)=106 dB

6.       Una cuerda de 8 metros de largo mantiene sus dos extremos fijos, y es sometida a una pulsación que produce una onda que tras rebotar en los extremos da lugar a una onda estacionaria con la ecuación: ψ(x,t)=4·sen(π/2 · x)·cos(π·t) (en cm)

a)     Escriba la ecuación de las ondas que dan origen a la onda estacionaria.

b)      Encuentra el valor de la longitud de onda y amplitud de las ondas.

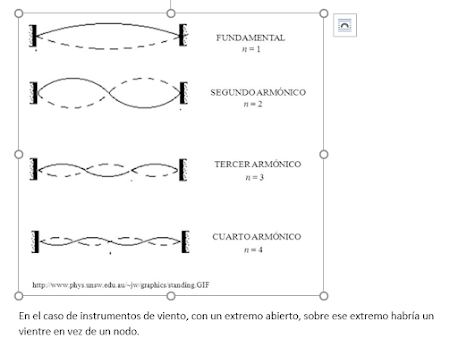
c)      Dada la longitud de la cuerda, ¿qué armónico se forma? Dibújalo. el caso de ondas sonoras en instrumentos de viento, con un extremo abierto, ¿qué encontramos en ese extremo?

Sabemos que ondas del tipo ψ(x,t)= A·sen(kx±wt), pueden dar origen a ondas estacionarias del tipo ψ(x,t)=2Asen(kx)cos(wt). Comparando las expresiones con el dato del ejercicio: ψ(x,t)=4·sen(π/2 · x)·cos(π·t), las ecuaciones de las dos ondas que darán origen a la estacionaria serán: ψ(x,t)=2·sen(π/2·x±πt) (cm)

La amplitud de la onda es 2 cm, y sabiendo que K=π/2 m^-1, calculamos λ.

λ=2π/K=4 metros.

Sabemos que la distancia entre nodos es la mitad de la longitud de onda, por tanto 2 metros. Como la cuerda mide 8 metros, existen además de los nodos de los extremos, tres nodos interiores en la posición x=2m, x=4m, x=6m. Por tanto, si consideramos que el estado fundamental admite la denominación de “primer armónico”, estaríamos con el cuarto armónico.