SOLUCIÓN EXAMEN ÓPTICA 2BACH FÍSICA 22-23

1. La luz se puede explicar como una onda. ¿De qué tipo es esta onda y cuál es su naturaleza? Es una onda electromagnética, de tipo transversal.

¿A qué velocidad se desplaza la luz? 300.000 Km/s ¿Qué ocurre con este valor de la velocidad? Sólo la luz puede viajar a esa velocidad, y constituye un límite que no puede ser superado para los objetos que forman el Universo.

Indica el nombre de una región del espectro de longitud de onda mayor que la luz. Repite para una región del espectro de longitud de onda menor que la luz.

Para el primer caso: infrarrojo, para el segundo caso ultravioleta.

3.    Un rayo de luz se dirige hacia un prisma de 27 grados de ángulo, entrando perpendicularmente como figura en el dibujo. Sabiendo que el prisma está hecho de un cristal de índice de refracción 1’40, encuentra los ángulos de reflexión o refracción del rayo dentro del prisma.

Primero calculamos el ángulo límite para la refracción entre cristal y el aire.

Para ello el ángulo de refracción sería de 90º.

n·sen(i_lim)=n’·sen(r )            n·sen(i_lim)=1·1      i_lim=arcsen(1/n)=45’6º

Ahora pasamos a abordar el problema, tambamos el prisma de forma que el ángulo esté a la derecha. El ángulo de incidencia, marcado en el dibujo es 63º

Al ser mayor 63º que el ángulo límite se producirá una reflexión interna, con un ángulo de 63º. El rayo se dirige hacia otra superficie de dioptrio, y la clave será saber si hay o no de nuevo una reflexión total. Debemos calcular el ángulo de incidencia en este otro caso, y ver si es mayor o menor que 42’5º.

Tenemos un triángulo auxiliar formado por la prolongación del rayo inicial y la normal de la segunda incidencia, y es n el que nos vamos a apoyar para calcular el segundo ángulo de incidencia. El primer triángulo amarillo, por ángulos suplementarios, vale 180-63-63=54º. El de incidencia, será el que complete los 180º del triángulo rectángulo: 180=90+54+i₂ à i₂=36º. Al ser menor que el límite se producirá una refracción que calculamos con ayuda de la Ley de Snell:

    nsen(I₂)=n’·sen(r₂)      sen(r₂)=1’4·sen(36)/1=0’823 à r₂=55’38º

La desviación del rayo será 90-55’37=34’62º.

4.                Un objeto se sitúa delante de un espejo cóncavo de radio 8 cm, produciendo una imagen con un aumento lateral de -0’8, encuentra las posiciones de la imagen y el objeto analíticamente, y clasifica la imagen. Construye un dibujo limpio del caso planteado con el trazado de los rayos.

 En los espejos, la focal es siempre la mitad del radio, en este caso f’=-4 cm por ser cóncavo.

 Ecuaciones de los espejos: 1/f’=1/s+1/s´                         m=-s’/s

En negrita, las incógnitas

 Como el radio es -8 cm, la focal es la mitad: f’=-4 cm. De la segunda ecuación obtenemos s’ en función de “s”, de forma que sería: s’= - m·s. Ahora sustituimos ese valor en la primera ecuación.

 1/f’= 1/s - 1/(ms) = 1/s – 1/(-0’8·s)=1/s+1/(0’8s) = 2’25/s

 s= f’·2’25 = - 9 cm

s’= - (-0’8)·(-9cm) = - 7’2 cm

LA IMAGEN ES MENOR E INVERTIDA, por ser el aumento lateral menor de la unidad y negativo. Y como se forma la imagen a la izquierda del espejo estará formada por los rayos verdaderos, por tanto, es una imagen real. Ver dibujo a continuación

La imagen está obtenida a partir del applet contenido en https://www.compadre.org/osp/EJSS/4431/225.htm

 

 

5.    Un objeto se sitúa a 8 cm de una lente DIVERGENTE de distancia focal imagen 4 cm en valor absoluto.

·      Calcula la posición de la imagen.

·      Clasifica la imagen producida.

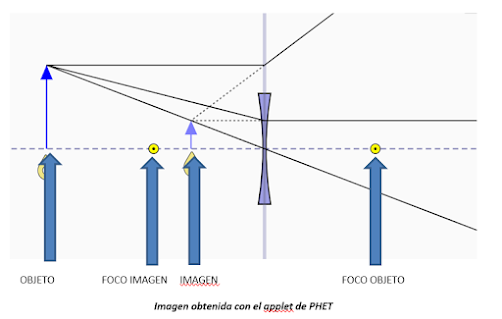
·      Haz el trazado de rayos. (No hace falta que el dibujo esté a escala, pero sí limpio y claro)

En las lentes divergentes, el foco imagen está a la izquierda de la lente, por tanto f’=-4cm (Ver dibujo posterior)

Aplicamos las ecuaciones de lentes, como sabemos la distancia objeto, s= - 8cm, podemos calcular directamente la distancia imagen.

1/f’=  - 1/s +  1/s´                         m=s’/s

1/s’=1/f’+1/s = (1/-4cm) + (1/-8cm)= -1/8-1/4=-3/8cm     Por tanto s’= - 8/3 cm = -2’66 cm

Aumento lateral: m=s’/s= (-2’66cm) / ( - 8cm) = + 0’332 Entonces la imagen es derecha por ser positiva y menor por ser un número menor de la unidad.

Como está a la izquierda de la lente, donde nunca van a estar los rayos refractados pero sí sus prolongaciones, será una imagen virtual.