1.
Una carga positiva de
masa “m” entra en una región donde hay un campo magnético uniforme “B” de forma perpendicular al mismo con una
velocidad “v”.
a. Dibuja la trayectoria que seguiría. [0,5 dibuja la
trayectoria limpia; 0,5 explica el porqué de la trayectoria]
b.
Dibuja las trayectorias,
(en escala aproximada, no tiene porqué ser exacta), que seguirían una carga de
igual masa y velocidad, pero de carga negativa; y una carga de igual carga y
velocidad, pero de masa triple. [0,5 dibuja la trayectorias limpias; 0,5 explica el porqué
de cada trayectoria]
Cuando una partícula cargada, con velocidad “v”, penetra en
un campo magnético de forma perpendicular al mismo, sufre una fuerza
perpendicular al campo y a la velocidad inicial cuyo valor es F=q·v·B, y que la
obliga a girar en el interior del campo magnético. Para conocer el sentido de
la fuerza aplicamos la regla de la mano izquierda:
Si varían la carga o la masa de la partícula, variará la
situación de la circunferencia trazada, o su tamaño. Si la carga es negativa,
pero de igual masa, la trayectoria será la misma, pero ahora el movimiento
circular será trazado en sentido de las agujas de reloj. La regla de la mano
izquierda está pensada para una carga positiva, si manejamos cargas negativas
debemos cambiar el sentido de la fuerza magnética.
Para averiguar lo que pasa
a una partícula positiva de masa triple que la primera, debemos primero
plantear cuánto vale el radio de giro, para ello hacemos uso de la segunda Ley
de Newton: F=m·a, como se trata de una aceleración centrípeta, a=v2/R.
F sabemos que vale F=q·v·B
Q·v·B=(m)v2/R Despejamos R y obtenemos: R=mv/(QB)
Esta sería la expresión a
aplicar para la primera partícula, nos daría un radio R al depejar. Si ahora
tenemos una masa triple: 3m…
Q·v·B=(3m)v2/R Despejamos R y vale: R=3mv/(QB)
Que es el triple que
antes. Dibujo la órbita de la primera partícula de azul, y la de la partícula
más masiva de violeta.
2.
Dos conductores paralelos de mismo sentido de corriente, por
los que circulan 3 y 7 amperios están separados 10 metros el uno del otro. [0,5 croquis indicando las magnitudes implicadas y los
vectores dibujados; 0,5 uso de unidades; 0,5 despeja y opera algebraicamente
antes de sustituir datos numéricos]
a. ¿En qué punto el
campo magnético creado por ambos se anula? [1
solución]
b.
¿Con qué fuerza se atraen/repelen ambos? [0,5 solución]
Representemos a los dos con ductores por dos círculos, como
si hubiéramos hecho un corte perpendicular a ambos. Como tienen el mismo
sentido de la corriente, supondremos que esta se introduce dentro de la
pantalla y por ello dentro de la circunferencia dibujamos un aspa.
Dibujamos igualmente las líneas del campo con ayuda de la
regla de la mano derecha, donde el pulgar simboliza el sentido de la corriente
y los dedos las líneas de fuerza del
campo magnético, las dibujamos de color amarillo.
Donde las dos
circunferencias, líneas de campo correspondientes a cada conductor, son
tangentes el campo total puede ser cero, ya que los campos de cada uno de ellas son de sentido opuesto.
Llamemos x a la distancia del primer conductor hasta ese punto
de tangencia de las líneas de campo. La distancia al otro conductor será
lógicamente 10-x.
Igualemos los módulos de los campo magnéticos,
para ello debemos saber el el valor del campo magnético creado por un conductor
a una distancia “x” vale: B=(µ0/2π)·I/x
B1=B2 à (µ0/2π)·I1 /x=(µ0/2π)·I2 /(10-x)
Eliminamos términos comunes:
I1 /x =I2
/ (10-x) Despejamos x
I1(10-x)=I2x 10·I1 –I1x = I2x 10·I1=x(I2+I1) x=10·I1/(I2+I1)=10cm·3A/10A=3m
El punto elegido estará a
3 m del primer conductor y a 7 m del segundo.
Dos conductores paralelos
de igual sentido de corriente se atraes con una fuerza por unidad de longitud…
(F/L)= (µ0/2π)·I1·I2/d=4π·10-7 (Tm/A)·3A·7A/(2·π·10m)=4,2·10-7N/m
3. Una espira circular
de 4 cm de radio se encuentra situada en frente de otra igual por la que
circula una corriente de 2 Amperios en el sentido de las agujas del reloj.
Indica qué ocurriría si:
a. Se aleja la primera
de la segunda. [0,5 conoce
respuesta];
b. Se acerca a la
segunda. [0,5 conoce
respuesta; 0,5 se explica bien haciendo uso de Leyes y términos físicos en
ambas respuestas, a y b]
c.
En la segunda espira repentinamente cesa de circular la
corriente eléctrica. [0,5 conoce
respuesta; 0,5 se explica bien haciendo uso de Leyes y términos físicos]
Para compensar la pérdida de flujo, en el circuito
número 1 se creará una corriente inducida que intentará generar las dos líneas
que faltan. La corriente inducida de azul y las líneas del campo inducido de
rojo.
Vamos al caso en el que el primer circuito se
acerca al segundo, ahora el flujo aumentará,
Ahora
aparecerá una corriente inducida que intentará crear un campo que se oponga al
del segundo circuito para que el flujo vuelva a ser 1:
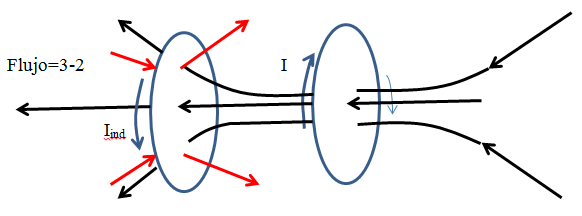
Finalmente
en el caso en que de forma inesperada desaparezca la corriente 2, entonces el
flujo magnético que atraviesa el circuito 1 pasa de valer 3 a valer 0, se
creará una corriente inducida que intente regenerar las líneas que falte:
4.
Se tienen 200 g de una muestra radiactiva cuya velocidad de
desintegración es tal que al cabo de un día sólo queda el 75% de la misma.
Calcula: La constante de desintegración, el período de semidesintegración y la
masa que quedará al cabo de 22 días.
[0,5 plantea ley de desintegración radiactiva, 0,5 relaciona los datos con
incógnita y despeja antes de sustituir datos numéricos; 0,5 cada resultado
correcto]
Aplicamos la ley de descomposición
radiactiva, que nos permite conocer los átomos que restan por descomponerse al
cabo de un tiempo “t”: N=N0·e-λt
A nosotros nos dan como dato la cantidad de
materia en gramos, la masa, pero eso no es problema porque la masa es
directamente proporcional al número de
átomos. Por tanto: m=m0·e-λt Donde m son las masas, m0 es la masa
inicial y λ la constante de desintegración radiactiva. Como el 75% de los
átomos no se han descompuesto, eso quiere decir que el 75% de la masa del
elemento radiactivo sigue allí al cabo de t=1día.
m=m0·e-λt=0,75m0
0,75=
e-λ·1día
-0,2877=-λ·1
día
λ=0,2877
dia-1
Conocida la constante de desinegración,
podemos calcular el período de semidesintegración:
T1/2=ln2/λ=2,409
días
La masa que restará al cabo de 22 días nos
obliga a volver a usar la ecuación de descomposición:
m=m0·e-λt=200g·e(-0,2877·22)=0,362g








Gracias por las explicaciones, son muy claras y me han ayudado mucho
ResponderEliminar